Lesson Plan Math Class 8 | Mensuration CH-14

E- LESSON PLAN SUBJECT MATHEMATICS CLASS- 8, CH-14

Lesson Plan for CBSE mathematics class 8 Mensuration, Step by step teaching strategy for mathematics teachers. Perfect lesson plan which makes the teaching learning process perfect

E-LESSON PLAN MATHEMATICS
CLASS-VIII
CHAPTER - 14 MENSURATION

RMB DAV CENTENARY PUBLIC SCHOOL NAWANSHAHR
NAME OF THE TEACHER				DINESH KUMAR
CLASS	VIII	CHAPTER	14	SUBJECT	MATHEMATICS
TOPIC	MENSURATION			DURATION : 15 Class Meetings

PREREQUISITE KNOWLEDGE FOR THIS LESSON PLAN

BASIC GEOMETRY:

Students should have a good understanding of basic geometric shapes like rectangles, squares, triangles, and circles.

PERIMETER AND AREA CONCEPTS:

Prior knowledge of the concepts of perimeter and area is essential. Students should understand that the perimeter is the total distance around a shape, while area represents the space enclosed by the shape.

MEASUREMENT UNITS:

Familiarity with measurement units like centimeters, meters, and square units (e.g., square centimeters, square meters) is necessary. This will enable them to work with measurements in real-world scenarios.

ARITHMETIC OPERATIONS:

A strong grasp of basic arithmetic operations, including addition, multiplication, and division, is important since these operations will be used in calculating perimeters and areas.

MATERIALS REQUIRED: 

Whiteboard and markers, Geometric shapes (e.g., cutouts or drawings), Worksheets with exercises.

LEARNING OBJECTIVES:

Students should be able to:

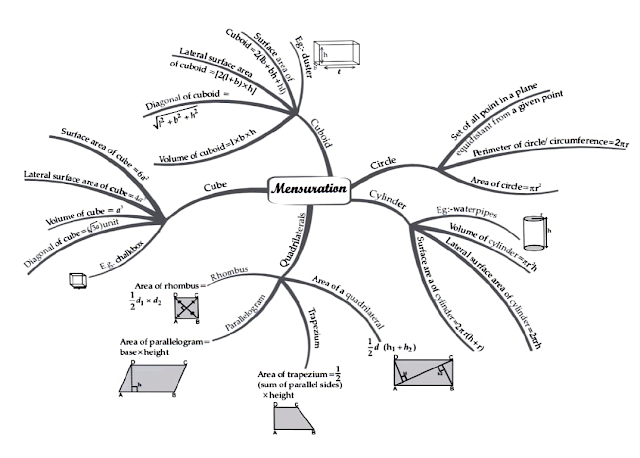
Define key mensuration terms, such as area, perimeter and volume.

Calculate the perimeter and area of basic geometric shapes (Quadrilateral, Trapezium, Parallelogram, Rectangle, Rhombus, square and triangle).

Apply the formulas for perimeter and area to solve real-world problems related to the above mentioned figures.

LEARNING OUTCOMES:

By the end of this lesson, students should:

Understand the concepts of perimeter and area of plane figureslike Quadrilateral, Trapezium, parallelogram, rectangle, rhombus and square.

Be able to calculate the perimeter and area of basic geometric shapes as mensioned above.

Be able to understand the surface area and volume of geometrical solid figures like: cube, cuboid, and cylinder.

Apply these concepts to solve practical problems in real-life situations.

RESOURCES

NCERT Text Book,

A Text Book of DAV Board

Resource Material : Worksheets , E-content, Basics and formulas from (cbsemathematics.com)

KEY TERMS 

Write the terms Perimeter, Area, Curved Surface Area, Lateral Surface Area, Volume, Quadrilateral, Trapezium, Parallelogram, Rectangle, Rhombus, Square, Cube, Cuboid, Cylinder on the board.

Define these terms:

Perimeter: The distance around a closed figure.

Area: The measure of the amount of space enclosed by a closed figure.

Discuss the importance of understanding perimeter and area in real-life situations.

PRESENTATION OF LESSON PLAN

PART-1 STATISTICS

INTRODUCTION : Greet the students and introduce the topic of mensuration.

Explain that mensuration is the branch of mathematics that deals with the measurement of geometric shapes (Plane Shapes and Solid Shapes) Like Triangle, Quadrilateral, Circle, Cube, Cuboid and Cylinder etc.

PERIMETER OF BASIC SHAPES 

Draw a rectangle on the board and label its sides.

Explain the formula for the perimeter of a rectangle: P = 2(l + b), where l is length and b is width.

Calculate the perimeter of the rectangle.

Repeat the process for a square, triangle and for other plane figures.

Encourage students to calculate the perimeters of these shapes on their own.

AREA OF BASIC SHAPES 

Draw a rectangle on the board again and label its sides.

Explain the formula for the area of a rectangle: A = l × b.

Calculate the area of the rectangle.

Repeat the process for a square, triangle  and other plane figures.

Encourage students to calculate the areas of these shapes on their own.

CUBE

Curved Surface area of cube = 4(side)²

Total surface area of cube = (side)²

Volume of Cube = (side)³

 Diagonal of Cube = √3(side)²

Number of faces = 6

Number of vertices = 8

Number of Edges = 12

Each face of a cube is a square

CUBOID

Curved Surface Area of cuboid = 2(l + b) ✖ h

Total Surface Area of cuboid = 2(lb + bh + hl)

Volume of cuboid = Length ✖ Breadth ✖ Height

Diagonal of  cuboid =   

Number of faces = 6  

Number of vertices = 8

Number of Edges = 12

Each face of a cube is a rectangle

CYLINDER

Curved Surface Area of cylinder = 2πrh

Total Surface Area of cylinder = 2πr(r + h)

Volume of cylinder = πr²h

Number of faces = 3 (One curved surface and two plane surface)

Number of vertices = 0

Number of edges = 2

MIND MAP

REAL-WORLD PROBLEM SOLVING 

Present a real-world problem that involves finding the perimeter or area of a geometric shape (e.g., a garden with a rectangular shape).

Ask students to work in pairs to solve the problem and present their solutions.

WORKSHEET PRACTICE 

Distribute worksheets with exercises related to finding perimeters and areas of basic shapes.

Allow students to work on the worksheets individually or in pairs.

Collect the worksheets for assessment.

CONCLUSION AND RECAP 

Review the key concepts covered in the lesson, perimeter, area, curved surface area, lateral surface area, volume and the formulas for plane figures and for solid figures.

Summarize the importance of these concepts in real life.

Ask if students have any questions or need clarification on any topic covered in the lesson.

HOMEWORK ASSIGNMENT

Assign homework exercises related to finding perimeters and areas of different plane shapes. Also assign an assignment related to the surface area and volumes of solid figures.

ASSESSMENT:

Assess students' understanding through class participation, worksheet completion, and their ability to solve real-world problems involving mensuration.

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW